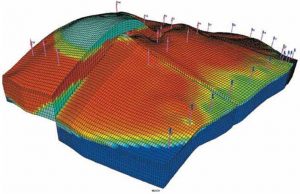
MPNF is an iterative solver for sparse linear equations arising from space and time discretization of fluid flow problems – such as those arising in oil reservoir simulation. The underlying grid may be structured or unstructured. It is designed to exploit the parallel processing capabilities of GPU-style processors, as supplied by companies such as NVIDIA, AMD and Intel. MPNF is a natural complement to the Multigrid methods often used in modern simulators – in many cases one excels where the other struggles.
Currently, MPNF is available as a DLL (Windows) or shared object (Linux) for NVIDIA GPUs. Some customization is likely to be required to integrate MPNF with client software. Please contact us to discuss possible applications of MPNF.
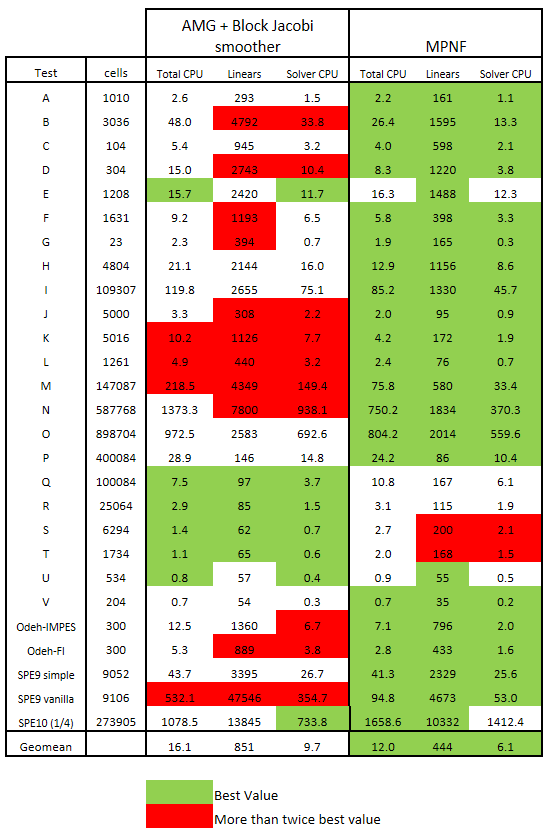
Anonymized MPNF Benchmarks
The table shows anonymized results of benchmark runs using a client oil reservoir simulator. It compares an existing arithmetic multi-grid (AMG) implementation of a CPR based solver with a block Jacobi smoother, to a full MPNF solver. In some problems a hybrid method, using AMG with an MPNF smoother provides the optimum performance.
Background
Dr. John Appleyard, one of the directors of Polyhedron Solutions, was one of the original authors of Eclipse, the oil reservoir simulator now developed and marketed by Schlumberger, which has been a dominant force in the industry for 30 years. He made numerous technical innovations, including the well-known Nested Factorization algorithm, which is used to solve the linear equations in Eclipse. In recent years, he has renewed his interest in linear solvers, and developed new solvers, including MPNF, which is designed to work best on massively parallel processors. Dr Appleyard holds two patents covering various aspects of this work.